Secp256k1: Difference between revisions
No edit summary |
Delete scamcoin promotion section →Cryptocurrencies |
||
| (9 intermediate revisions by 6 users not shown) | |||
| Line 1: | Line 1: | ||
'''secp256k1''' refers to the parameters of the | [[File:Secp256k1.png|thumb |This is a graph of secp256k1's elliptic curve ''y<sup>2</sup> = x<sup>3</sup> + 7'' over the real numbers. Note that because secp256k1 is actually defined over the field Z<sub>p</sub>, its graph will in reality look like random scattered points, not anything like this.]] | ||
'''secp256k1''' refers to the parameters of the elliptic curve used in Bitcoin's public-key cryptography, and is defined in ''Standards for Efficient Cryptography (SEC)'' (Certicom Research, http://www.secg.org/sec2-v2.pdf). Currently Bitcoin uses secp256k1 with the [[ECDSA]] algorithm, though the same curve with the same public/private keys can be used in some other algorithms such as [[Schnorr]]. | |||
secp256k1 was almost never used before Bitcoin became popular, but it is now gaining in popularity due to its several nice properties. Most commonly-used curves have a random structure, but secp256k1 was constructed in a special non-random way which allows for especially efficient computation. As a result, it is often more than 30% faster than other curves if the implementation is sufficiently optimized. Also, unlike the popular NIST curves, secp256k1's constants were selected in a predictable way, which significantly reduces the possibility that the curve's creator inserted any sort of backdoor into the curve. | |||
=== Technical details === | |||
As excerpted from ''Standards'': | As excerpted from ''Standards'': | ||
| Line 19: | Line 25: | ||
* ''n'' = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 | * ''n'' = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141 | ||
* ''h'' = 01 | * ''h'' = 01 | ||
=== Properties === | |||
* secp256k1 has characteristic ''p'', it is defined over the prime field ℤ<sub>''p''</sub>. Some other curves in common use have characteristic ''2'', and are defined over a binary Galois field ''GF(2<sup>n</sup>)'', but secp256k1 is not one of them. | |||
* As the ''a'' constant is zero, the ''ax'' term in the curve equation is always zero, hence the curve equation becomes ''y<sup>2</sup> = x<sup>3</sup> + 7''. | |||
== See also == | |||
* [https://bitcoin.stackexchange.com/questions/21907/what-does-the-curve-used-in-bitcoin-secp256k1-look-like What does secp256k1 look like] (Bitcoin stack exchange answer by Pieter Wuille) | |||
[[es:Secp256k1]] | |||
[[Category:Technical]] | |||
Latest revision as of 00:14, 24 April 2019
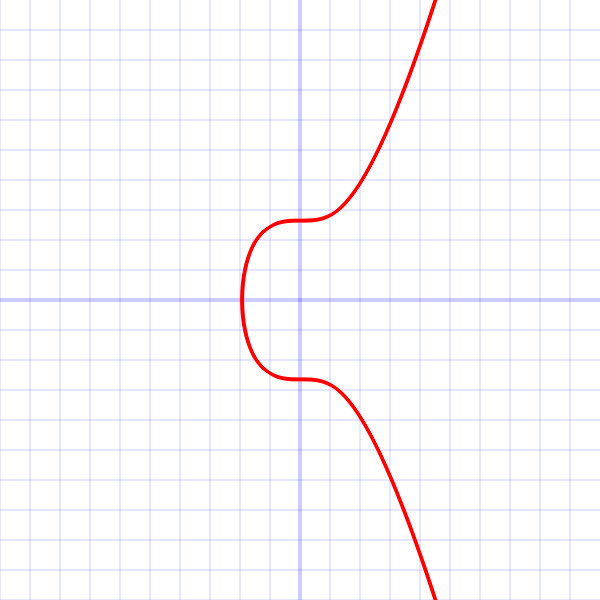
secp256k1 refers to the parameters of the elliptic curve used in Bitcoin's public-key cryptography, and is defined in Standards for Efficient Cryptography (SEC) (Certicom Research, http://www.secg.org/sec2-v2.pdf). Currently Bitcoin uses secp256k1 with the ECDSA algorithm, though the same curve with the same public/private keys can be used in some other algorithms such as Schnorr.
secp256k1 was almost never used before Bitcoin became popular, but it is now gaining in popularity due to its several nice properties. Most commonly-used curves have a random structure, but secp256k1 was constructed in a special non-random way which allows for especially efficient computation. As a result, it is often more than 30% faster than other curves if the implementation is sufficiently optimized. Also, unlike the popular NIST curves, secp256k1's constants were selected in a predictable way, which significantly reduces the possibility that the curve's creator inserted any sort of backdoor into the curve.
Technical details
As excerpted from Standards:
The elliptic curve domain parameters over Fp associated with a Koblitz curve secp256k1 are specified by the sextuple T = (p,a,b,G,n,h) where the finite field Fp is defined by:
- p = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
- = 2256 - 232 - 29 - 28 - 27 - 26 - 24 - 1
The curve E: y2 = x3+ax+b over Fp is defined by:
- a = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000000
- b = 00000000 00000000 00000000 00000000 00000000 00000000 00000000 00000007
The base point G in compressed form is:
- G = 02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
and in uncompressed form is:
- G = 04 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 483ADA77 26A3C465 5DA4FBFC 0E1108A8 FD17B448 A6855419 9C47D08F FB10D4B8
Finally the order n of G and the cofactor are:
- n = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE BAAEDCE6 AF48A03B BFD25E8C D0364141
- h = 01
Properties
- secp256k1 has characteristic p, it is defined over the prime field ℤp. Some other curves in common use have characteristic 2, and are defined over a binary Galois field GF(2n), but secp256k1 is not one of them.
- As the a constant is zero, the ax term in the curve equation is always zero, hence the curve equation becomes y2 = x3 + 7.
See also
- What does secp256k1 look like (Bitcoin stack exchange answer by Pieter Wuille)