RIPEMD-160
RIPEMD-160 is a cryptographic hash function based upon the Merkle–Damgård construction. It is used in the Bitcoin standard. It is a a strengthened version of the RIPEMD algorithm which produces a 128 bit hash digest while the RIPEMD-160 algorithm produces a 160-bit output. The compression function is made up of 80 stages made up of 5 blocks that run 16 times each. This pattern runs twice with the results being combined at the bottom using modulo 32 addition.
Padding
The compression function works upon 16 32-bit unsigned words. This requires the message to be padded to a multiple of 512 bits and the byte stream input to be padded into 32-bit words. The padding scheme is identical to MD4 using Merkle–Damgård strengthening to prevent length extension attacks. This consists of a one being added to the end of the message and the length of the message (in bits) being added to the end of the block. The bytes are pushed into the word low end first. Here are 4 examples of messages being padded into a word to show the possible patterns for different message lengths:

The length of the message should then be added to the second to last element (the length is saved a 64-bit value across the last 2 words, but it is unlikely the message will be this long; 32-bits will certainly suffice for Bitcoin software.)
Compression Function

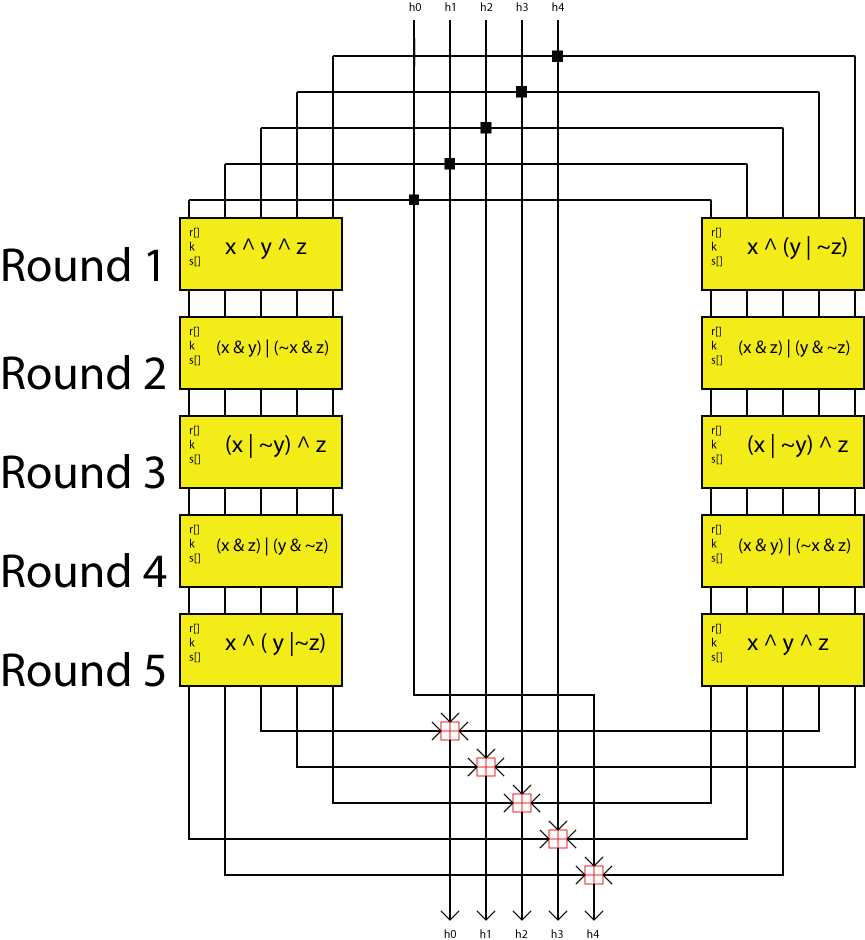
The compression function is made up of a variable sub block that the message block is passed though 16 times. There are 5 different variations for a total of 80 runs. This process occurs twice with the data meeting at the bottom to be moved on to the next block (if there is one) or added to the hash register is there isn't. The sub block can be varied by the design of a nonlinear function, the order in which the message block is read in per round, the amount of a left rotate and a k constant. The design of the sub block and the overall layout of the compression function is shown to the right.
Pseudocode for the process:
for(i := 0 to blocks - 1) {
aLeft := h0
bLeft := h1
cLeft := h2
dLeft := h3
eLeft := h4
aRight := h0
bRight := h1
cRight := h2
dRight := h3
eRight := h4
for(int j := 0 to 79) {
t := rotleft(s[j]) (aLeft + f(bLeft, cLeft, dLeft) + X[r[i]]) + eLeft
aLeft := eLeft;
eLeft := dLeft
dLeft := rotleft(10) (c)
cLeft := bLeft
bLeft := t
Do same for right
}
t := h1 + cLeft + dRight
h1 := h2 + dLeft + eRight
h2 := h3 + eLeft + aRight
h3 := h4 + aLeft + bRight
h4 := h0 + bLeft + cRight
h0 := t
}
The nonlinear functions are applied in the opposite directions up and down the left and right lines. The design of the functions from top to bottom on the left and bottom to top on the right are (Java syntax for operations):
- x ^ y ^ z
- (x & y) | (~x & z)
- (x | ~y) ^ z
- (x & z) | (y & ~z)
- z ^ (y | ~z)
The k values for left from top to bottom are:
- 0x00000000
- 0x5A827999
- 0x6ED9EBA1
- 0X8F1BBCDC
- 0XA953FD4E
The k values for right from top to bottom are:
- 0x50A28BE6
- 0x5C4DD124
- 0x6D703EF3
- 0x7A6D76E9
- 0x00000000
The order in which the words should be selected from the block array X for the left hand side are (each sub array within the 2D array represents a round. The array at the top represents the round at the top and the array at the bottom represents the round at the bottom):
{{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15}, //Round 1
{7, 4, 13, 1, 10, 6, 15, 3, 12, 0, 9, 5, 2, 14, 11, 8}, //Round 2
{3, 10, 14, 4, 9, 15, 8, 1, 2, 7, 0, 6, 13, 11, 5, 12}, //Round 3
{1, 9, 11, 10, 0, 8, 12, 4, 13, 3, 7, 15, 14, 5, 6, 2}, //Round 4
{4, 0, 5, 9, 7, 12, 2, 10, 14, 1, 3, 8, 11, 6, 15, 13}} //Round 5
The order in which the words should be selected from the array X for the right hand side are (following the same pattern as above):
{{5, 14, 7, 0, 9, 2, 11, 4, 13, 6, 15, 8, 1, 10, 3, 12}, //Round 1
{6, 11, 3, 7, 0, 13, 5, 10, 14, 15, 8, 12, 4, 9, 1, 2}, //Round 2
{15, 5, 1, 3, 7, 14, 6, 9, 11, 8, 12, 2, 10, 0, 4, 13}, //Round 3
{8, 6, 4, 1, 3, 11, 15, 0, 5, 12, 2, 13, 9, 7, 10, 14}, //Round 4
{12, 15, 10, 4, 1, 5, 8, 7, 6, 2, 13, 14, 0, 3, 9, 11}} //Round 5
The order of the left rotates on the left hand side are:
{{11, 14, 15, 12, 5, 8, 7, 9, 11, 13, 14, 15, 6, 7, 9, 8}, //Round 1
{7, 6, 8, 13, 11, 9, 7, 15, 7, 12, 15, 9, 11, 7, 13, 12}, //Round 2
{11, 13, 6, 7, 14, 9, 13, 15, 14, 8, 13, 6, 5, 12, 7, 5}, //Round 3
{11, 12, 14, 15, 14, 15, 9, 8, 9, 14, 5, 6, 8, 6, 5, 12}, //Round 4
{9, 15, 5, 11, 6, 8, 13, 12, 5, 12, 13, 14, 11, 8, 5, 6}} //Round 5
The order of the left rotates on the right hand side are:
{{8, 9, 9, 11, 13, 15, 15, 5, 7, 7, 8, 11, 14, 14, 12, 6}, //Round 1
{9, 13, 15, 7, 12, 8, 9, 11, 7, 7, 12, 7, 6, 15, 13, 11}, //Round 2
{9, 7, 15, 11, 8, 6, 6, 14, 12, 13, 5, 14, 13, 13, 7, 5}, //Round 3
{15, 5, 8, 11, 14, 14, 6, 14, 6, 9, 12, 9, 12, 5, 15, 8}, //Round 4
{8, 5, 12, 9, 12, 5, 14, 6, 8, 13, 6, 5, 15, 13, 11, 11}}; //Round 5