Quantum computing and Bitcoin: Difference between revisions
Adding more details regarding timelines |
m Improved Nerem-Gaur formula |
||
| (One intermediate revision by the same user not shown) | |||
| Line 7: | Line 7: | ||
The most dangerous attack by quantum computers is against public-key cryptography. On traditional computers, it takes on the order of 2<sup>128</sup> basic operations to get the Bitcoin private key associated with a Bitcoin public key. This number is so massively large that any attack using traditional computers is completely impractical. However, it is known for sure that it would take a sufficiently large quantum computer on the order of only 128<sup>3</sup> basic quantum operations to be able to break a Bitcoin key using Shor's Algorithm. This might take some time, especially since the first quantum computers are likely to be extremely slow, but it is still very practical. | The most dangerous attack by quantum computers is against public-key cryptography. On traditional computers, it takes on the order of 2<sup>128</sup> basic operations to get the Bitcoin private key associated with a Bitcoin public key. This number is so massively large that any attack using traditional computers is completely impractical. However, it is known for sure that it would take a sufficiently large quantum computer on the order of only 128<sup>3</sup> basic quantum operations to be able to break a Bitcoin key using Shor's Algorithm. This might take some time, especially since the first quantum computers are likely to be extremely slow, but it is still very practical. | ||
For symmetric cryptography, quantum attacks exist, but are less dangerous. Using Grover's Algorithm, the number of operations required to attack a symmetric algorithm is square-rooted. For example, finding some data which hashes to a specific SHA-256 hash requires 2<sup>256</sup> basic operations on a traditional computer, but 2<sup>128</sup> basic quantum operations. Both of these are impractically large. Also, since quantum computers will be massively slower and more expensive than traditional computers for decades after they | For symmetric cryptography, quantum attacks exist, but are less dangerous. Using Grover's Algorithm, the number of operations required to attack a symmetric algorithm is square-rooted. For example, finding some data which hashes to a specific SHA-256 hash requires 2<sup>256</sup> basic operations on a traditional computer, but 2<sup>128</sup> basic quantum operations. Both of these are impractically large. Also, since quantum computers will be massively slower and more expensive than traditional computers for decades after they were invented, quantum attacks against symmetric crypto seem unlikely to be especially common. If quantum computers grow in speed and shrink in price over time, then their inherent per-operation advantage in mining might allow them to out-compete classical computers in Bitcoin mining at some point. | ||
=== Timeline / plausibility === | === Timeline / plausibility === | ||
Creating a quantum computer is a ''massive'' scientific and engineering challenge. As of 2019, the largest general-purpose quantum computers have fewer than 100 qubits, have impractically | Creating a quantum computer is a ''massive'' scientific and engineering challenge. As of 2019, the largest general-purpose quantum computers have fewer than 100 qubits, have impractically high error rates, and can operate only in lab conditions at temperatures near absolute zero. Attacking Bitcoin keys would require around 1500 qubits. Humanity currently does not have the technology necessary to create a quantum computer large enough to attack Bitcoin keys. It is not known how quickly this technology will advance; however, cryptography standards such as ECRYPT II tend to say that Bitcoin's 256-bit ECDSA keys are secure until at least 2030-2040. As of 2024, according to BTQ's quantum risk calculator <ref> https://qrc.btq.li/ </ref>, breaking BitECDSA using Shor's algorithm could happen as early as 2032 under optimistic assumptions, and as far as 2048 under pessimistic ones. An in-depth analysis was presented in <ref> Aggarwal, D., Brennen, G., Lee, T., Santha, M., & Tomamichel, M. (2018). Quantum Attacks on Bitcoin, and How to Protect Against Them. Ledger, 3. https://doi.org/10.5195/ledger.2018.127 </ref> | ||
There is a company called D-Wave | There is a company called D-Wave that claims to produce quantum computers with over 2000 qubits. However, this claim has not been universally accepted, and even if it is true, this is a ''special-purpose'' "annealing quantum processor" incapable of attacking crypto. | ||
== Quantum mining == | == Quantum mining == | ||
A miner with quantum hardware can use Grover's algorithm, to gain a quadratic | A miner with quantum hardware can use Grover's algorithm, to gain a quadratic advantage: By applying t Grover iterations, the probability of finding a successful block scales like t<sup>2</sup>; this should be compared with a classical miner, which by applying t iterations the probability scales linearly with t. The ramifications of this difference were analyzed in several works. | ||
A quantum miner may choose how many Grover iterations to apply. Classical miners switch to a new block whenever they hear about it. A quantum miner, which learn about a new block, would be better to first measure their own block before switching. It turns out that this phenomenon will increase the fork-rate. In order to mitigate this problem, a different tie-breaking rule was suggested<ref>Sattath, O. On the insecurity of quantum Bitcoin mining. Int. J. Inf. Secur. 19, 291–302 (2020). https://doi.org/10.1007/s10207-020-00493-9 </ref>. The strategy which quantum miners should use, even under this modified tie-breaking rule, is only partially understood<ref> Troy Lee, Maharshi Ray, and Miklos Santha. Strategies for Quantum Races. In 10th Innovations in Theoretical Computer Science Conference (ITCS 2019). Leibniz International Proceedings in Informatics (LIPIcs), Volume 124, pp. 51:1-51:21, Schloss Dagstuhl – Leibniz-Zentrum für Informatik (2019) | A quantum miner may choose how many Grover iterations to apply. Classical miners switch to a new block whenever they hear about it. A quantum miner, which learn about a new block, would be better to first measure their own block before switching. It turns out that this phenomenon will increase the fork-rate. In order to mitigate this problem, a different tie-breaking rule was suggested<ref>Sattath, O. On the insecurity of quantum Bitcoin mining. Int. J. Inf. Secur. 19, 291–302 (2020). https://doi.org/10.1007/s10207-020-00493-9 </ref>. The strategy which quantum miners should use, even under this modified tie-breaking rule, is only partially understood<ref> Troy Lee, Maharshi Ray, and Miklos Santha. Strategies for Quantum Races. In 10th Innovations in Theoretical Computer Science Conference (ITCS 2019). Leibniz International Proceedings in Informatics (LIPIcs), Volume 124, pp. 51:1-51:21, Schloss Dagstuhl – Leibniz-Zentrum für Informatik (2019) | ||
https://doi.org/10.4230/LIPIcs.ITCS.2019.51 </ref>: the main part missing in the analysis is that this work finds the equilibrium strategy when considering quantum mining as a single-shot game, wehreas in practice, it is a repeated game. Furtheremore, this work assumes that the different quantum miners are symmetric, with full knowledge of the hash-rate of the others, which is unrealistic assumption in a decentralized system. | https://doi.org/10.4230/LIPIcs.ITCS.2019.51 </ref>: the main part missing in the analysis is that this work finds the equilibrium strategy when considering quantum mining as a single-shot game, wehreas in practice, it is a repeated game. Furtheremore, this work assumes that the different quantum miners are symmetric, with full knowledge of the hash-rate of the others, which is unrealistic assumption in a decentralized system. | ||
A form of a 51% attack, with a single quantum miner was | A form of a 51% attack, with a single quantum miner was proposed in Ref.<ref> Bailey, B., & Sattath, O. (2024). 51% Attack via Difficulty Increase with a Small Quantum Miner. arXiv preprint https://arxiv.org/abs/2403.08023 </ref>. In the attack, the quantum miner ''increases'' the difficulty. Since Bitcoin nodes follow the chain with the most commutative proof of work, an increase by a factor of c is only square root of c harder to mine for the quantum miner, but counts as c blocks. Implementing this attack would require extremely fast, noise tolearant quantum computers (with a clock rate exceeding the fastest classical computers available as of 2024), and therefore is considered only a long term concern. | ||
It may seem hard to know whether a quantum miner joins the network. Perhaps surprisingly, in Ref. <ref> Nerem, R. R., & Gaur, D. R. (2023). Conditions for advantageous quantum Bitcoin mining. Blockchain: Research and Applications, 4(3), 100141. https://doi.org/10.1016/j.bcra.2023.100141 </ref> it was shown that the optimal mining time for the first small quantum miner that joins has a closed form formula: | |||
[[File:Gerem-Naur_optimal_mining_minutes.png]] | |||
In the equation above, W is Lambert's W-function, and λ<sub>0</sub> is the expected block time. This means that seeing too many blocks mined after 15.593 minutes after the previous blocks could be a signal that quantum mining has started. | |||
== Mitigations == | == Mitigations == | ||
Revision as of 08:22, 2 May 2024
Quantum computers are computers which exploit quantum mechanics to do certain computations far more quickly than traditional computers. A sufficiently large quantum computer would cause some trouble for Bitcoin, though it would certainly not be insurmountable.
Note that the abbreviation QC can stand for either quantum computer(s) or quantum cryptography.
QC attacks
The most dangerous attack by quantum computers is against public-key cryptography. On traditional computers, it takes on the order of 2128 basic operations to get the Bitcoin private key associated with a Bitcoin public key. This number is so massively large that any attack using traditional computers is completely impractical. However, it is known for sure that it would take a sufficiently large quantum computer on the order of only 1283 basic quantum operations to be able to break a Bitcoin key using Shor's Algorithm. This might take some time, especially since the first quantum computers are likely to be extremely slow, but it is still very practical.
For symmetric cryptography, quantum attacks exist, but are less dangerous. Using Grover's Algorithm, the number of operations required to attack a symmetric algorithm is square-rooted. For example, finding some data which hashes to a specific SHA-256 hash requires 2256 basic operations on a traditional computer, but 2128 basic quantum operations. Both of these are impractically large. Also, since quantum computers will be massively slower and more expensive than traditional computers for decades after they were invented, quantum attacks against symmetric crypto seem unlikely to be especially common. If quantum computers grow in speed and shrink in price over time, then their inherent per-operation advantage in mining might allow them to out-compete classical computers in Bitcoin mining at some point.
Timeline / plausibility
Creating a quantum computer is a massive scientific and engineering challenge. As of 2019, the largest general-purpose quantum computers have fewer than 100 qubits, have impractically high error rates, and can operate only in lab conditions at temperatures near absolute zero. Attacking Bitcoin keys would require around 1500 qubits. Humanity currently does not have the technology necessary to create a quantum computer large enough to attack Bitcoin keys. It is not known how quickly this technology will advance; however, cryptography standards such as ECRYPT II tend to say that Bitcoin's 256-bit ECDSA keys are secure until at least 2030-2040. As of 2024, according to BTQ's quantum risk calculator [1], breaking BitECDSA using Shor's algorithm could happen as early as 2032 under optimistic assumptions, and as far as 2048 under pessimistic ones. An in-depth analysis was presented in [2]
There is a company called D-Wave that claims to produce quantum computers with over 2000 qubits. However, this claim has not been universally accepted, and even if it is true, this is a special-purpose "annealing quantum processor" incapable of attacking crypto.
Quantum mining
A miner with quantum hardware can use Grover's algorithm, to gain a quadratic advantage: By applying t Grover iterations, the probability of finding a successful block scales like t2; this should be compared with a classical miner, which by applying t iterations the probability scales linearly with t. The ramifications of this difference were analyzed in several works.
A quantum miner may choose how many Grover iterations to apply. Classical miners switch to a new block whenever they hear about it. A quantum miner, which learn about a new block, would be better to first measure their own block before switching. It turns out that this phenomenon will increase the fork-rate. In order to mitigate this problem, a different tie-breaking rule was suggested[3]. The strategy which quantum miners should use, even under this modified tie-breaking rule, is only partially understood[4]: the main part missing in the analysis is that this work finds the equilibrium strategy when considering quantum mining as a single-shot game, wehreas in practice, it is a repeated game. Furtheremore, this work assumes that the different quantum miners are symmetric, with full knowledge of the hash-rate of the others, which is unrealistic assumption in a decentralized system.
A form of a 51% attack, with a single quantum miner was proposed in Ref.[5]. In the attack, the quantum miner increases the difficulty. Since Bitcoin nodes follow the chain with the most commutative proof of work, an increase by a factor of c is only square root of c harder to mine for the quantum miner, but counts as c blocks. Implementing this attack would require extremely fast, noise tolearant quantum computers (with a clock rate exceeding the fastest classical computers available as of 2024), and therefore is considered only a long term concern.
It may seem hard to know whether a quantum miner joins the network. Perhaps surprisingly, in Ref. [6] it was shown that the optimal mining time for the first small quantum miner that joins has a closed form formula:
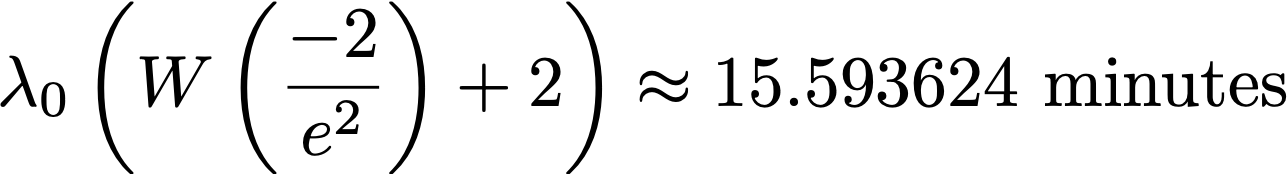
In the equation above, W is Lambert's W-function, and λ0 is the expected block time. This means that seeing too many blocks mined after 15.593 minutes after the previous blocks could be a signal that quantum mining has started.
Mitigations
Bitcoin already has some built-in quantum resistance. If you only use Bitcoin addresses one time, which has always been the recommended practice, then your ECDSA public key is only ever revealed at the one time that you spend bitcoins sent to each address. A quantum computer would need to be able to break your key in the short time between when your transaction is first sent and when it gets into a block. It will likely be decades after a quantum computer first breaks a Bitcoin key before quantum computers become this fast.
All of the commonly-used public-key algorithms are broken by QC. This includes RSA, DSA, DH, and all forms of elliptic-curve cryptography. Public-key crypto that is secure against QC does exist, however. Currently, Bitcoin experts tend to favor a cryptosystem based on Lamport signatures. Lamport signatures are very fast to compute, but they have two major downsides:
- The signature would be quite large, at least several kB (40-170 times larger than now). This would be very bad for Bitcoin's overall scalability, since bandwidth is one of the main limiting factors to Bitcoin's scaling. Advances in scalability such as Segregated Witness (the signature is part of the witness) and Lightning will be helpful.
- At the time that you create each keypair, you would need to set some finite maximum number of times that you can sign with this key. Signing more than this number of times would be insecure. Increasing the signing limit increases the size of each signature even more. Since you are only really supposed to use addresses once, this may not be a huge problem for Bitcoin.
There is also some ongoing academic research on creating quantum-safe public-key algorithms with many of the same properties as today's public-key algorithms, but this is very experimental. It is not known whether it will end up being possible.
A new public-key algorithm can be added to Bitcoin as a softfork. From the end-user perspective, this would appear as the creation of a new address type, and everyone would need to send their bitcoins to this new address type to achieve quantum security.
See Also
- ↑ https://qrc.btq.li/
- ↑ Aggarwal, D., Brennen, G., Lee, T., Santha, M., & Tomamichel, M. (2018). Quantum Attacks on Bitcoin, and How to Protect Against Them. Ledger, 3. https://doi.org/10.5195/ledger.2018.127
- ↑ Sattath, O. On the insecurity of quantum Bitcoin mining. Int. J. Inf. Secur. 19, 291–302 (2020). https://doi.org/10.1007/s10207-020-00493-9
- ↑ Troy Lee, Maharshi Ray, and Miklos Santha. Strategies for Quantum Races. In 10th Innovations in Theoretical Computer Science Conference (ITCS 2019). Leibniz International Proceedings in Informatics (LIPIcs), Volume 124, pp. 51:1-51:21, Schloss Dagstuhl – Leibniz-Zentrum für Informatik (2019) https://doi.org/10.4230/LIPIcs.ITCS.2019.51
- ↑ Bailey, B., & Sattath, O. (2024). 51% Attack via Difficulty Increase with a Small Quantum Miner. arXiv preprint https://arxiv.org/abs/2403.08023
- ↑ Nerem, R. R., & Gaur, D. R. (2023). Conditions for advantageous quantum Bitcoin mining. Blockchain: Research and Applications, 4(3), 100141. https://doi.org/10.1016/j.bcra.2023.100141